Penerapan Sistem Bilangan Digital
Sistem Bilangan Digital
Banyak sistem-sistem bilangan yang
digunakan pada teknologi digital. Yang paling umum adalah sistem-sistem
desimal, biner, oktal dan heksadesimal. Sistem desimal adalah yang
banyak dikenal karena sering digunakan setiap hari. Dengan mempelajari
karakteristiknya akan membantu memahami sistem-sistem bilangan lain
secara lebih baik.
Sistem desimal tersusun atas 10 angka
atau simbol, yang dikenal dengan digit. Ke-10 simbol ini adalah 0, 1,
2, 3, 4, 5, 6, 7, 8, 9. Sistem desimal juga disebut sistem basis-10, karena mempunyai 10 digit. Kenyataannya, kata ”digit” adalah kata latin yang berarti ”jari-jari”.
Sistem desimal adalah suatu sistem nilai posisional di
mana nilai dari suatu digit tergantung kepada posisinya. Misalnya
perhatikanlah bilangan desimal 634 ini artinya digit 4 sesungguhnya
menyatakan 4 satuan. 3 menyatakan 3 puluhan dan 6 menyatakan 6 ratusan.
Ringkasnya, 6 merupakan yang paling berbobot dari ketiga digit, dikenal
sebagai Most Significant Digit (MSD). 4 bobotnya paling kecil dan
disebut Least Significant Digit (LSD). Perhatikan contoh lain, 75.25.
Bilangan ini sesungguhnya sama dengan tujuh puluh plus lima satuan plus
dua persepuluh plus lima perseratus.
Hampir semua sistem digital
menggunakan sistem bilangan biner sebagai dasar sistem bilangan dari
operasinya, meskipun sistem-sistem bilangan lain sering digunakan
secara bersama-sama dengan biner. Dengan menggunakan 2 level yang ada
pada sistem biner maka sangatlah mudah untuk mendesain rangkaian –
rangkaian elektronik yang akurat dibandingkan dengan menggunakan 10
level yang ada pada sistem desimal.
Dalam
sistem biner, hanya ada 2 simbol atau digit yaitu 0 dan 1 yang dikenal
juga dengan system basis-2. Sistem biner ini dapat digunakan untuk
menyatakan setiap kuantitas yang dapat dinyatakan dalam desimal atau
sistem bilangan yang lainnya.
Sistem
biner juga suatu sistem nilai posisional, dimana tiap-tiap digit biner
mempunyai nilainya sendiri atau bobot yang dinyatakan sebagai pangkat
2.
Tabel berikut menunjukkan urutan hitungan pada system bilangan biner.3. Menyatakan Kuantitas-Kuantitas Biner
Dalam system digital informasi yang
akan diproses biasanya dinyatakan dalam bentuk biner. Kuantitas biner
dapat dinyatakan dengan setiap alat yang hanya mempunyai dua kondisi
kerja. Sebagai contoh sebuah saklar yang hanya mempunyai kondisi
terbuka yang menyatakan biner 0 atau kondisi tertutup yang menyatakan
biner 1.
Gambar 1. Menggunakan saklar untuk menyatakan bilangan-bilangan biner
Pada
sistem-sistem digital elektronik, informasi biner dinyatakan oleh
sinyal-sinyal listrik yang terdapat pada input dan output dari berbagai
macam rangkaian-rangkaian elektronik. Dalam sistem ini, biner 0 dan 1
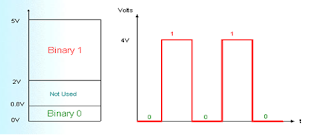
dinyatakan oleh dua tegangan yang ekstrim berlawanan. Misalnya biner 0
dapat dinyatakan dengan harga nominal 0 volt dan biner 1 dinyatakan
dengan 5 volt. Untuk lebih jelasnya perhatikan gambar 1.5 berikut.
Biner 1 : tegangan antara 2V sampai 5VBiner 0 : tegangan antara 0V sampai 0.8 V
Tegangan antara 0.8V sampai 2V tidak digunakan, karena akan menyebabkan kesalahan dalam rangkaian digital.
Gambar 1. Bentuk sinyal digita
MATERI KE 2
Sistem Bilangan Digital
Sistem bilangan desimal adalah sistem bilangan yang
menggunakan 10 macam angka dari 0,1, sampai 9. Setelah angka 9, angka
berikutnya adalah 1 0, 1 1, dan seterusnya (posisi di angka 9 diganti
dengan angka 0, 1, 2, .. 9 lagi, tetapi angka di depannya dinaikkan
menjadi 1). Sistem bilangan desimal sering dikenal sebagai sistem
bilangan berbasis 10, karena tiap angka desimal menggunakan basis
(radix) 10, seperti yang terlihat dalam contoh berikut:
angka desimal 123 = 1*102 + 2*101 + 3*100
sistem
bilangan biner(basis 2), sistem bilangan/ angka oktal (basis 8), dan
sistem angka heksadesimal (basis 16) yang merupakan dasar pengetahuan
untuk mempelajari komputer digital. Bilangan oktal dibentuk dari
bilangan biner-nya dengan mengelompokkan tiap 3 bit dari ujung kanan
(LSB). Sementara bilangan heksadesimal juga dapat dibentuk dengan mudah
dari angka biner-nya dengan mengelompokkan tiap 4 bit dari ujung kanan.
Oktal atau sistem bilangan basis 8
adalah sebuah sistem bilangan berbasis delapan. Simbol yang digunakan
pada sistem ini adalah 0,1,2,3,4,5,6,7. Konversi Sistem Bilangan Oktal
berasal dari Sistem bilangan biner yang dikelompokkan tiap tiga bit
biner dari ujung paling kanan (LSB atau Least Significant Bit).
Sistem bilangan biner atau sistem bilangan basis dua
adalah sebuah sistem penulisan angka dengan menggunakan dua simbol
yaitu 0 dan 1. Sistem bilangan biner modern ditemukan oleh Gottfried
Wilhelm Leibniz pada abad ke-17. Sistem bilangan ini merupakan dasar
dari semua sistem bilangan berbasis digital. Dari sistem biner, kita
dapat mengkonversinya ke sistem bilangan Oktal atau Hexadesimal. Sistem
ini juga dapat kita sebut dengan istilah bit, atau Binary Digit. Pengelompokan biner dalam komputer selalu berjumlah 8, dengan istilah 1 Byte/bita. Dalam istilah komputer, 1 Byte = 8 bit. Kode-kode rancang bangun komputer, seperti ASCII, American Standard Code for Information Interchange menggunakan sistem peng-kode-an 1 Byte.
Heksadesimal atau sistem bilangan basis 16
adalah sebuah sistem bilangan yang menggunakan 16 simbol. Berbeda
dengan sistem bilangan desimal, simbol yang digunakan dari sistem ini
adalah angka 0 sampai 9, ditambah dengan 6 simbol lainnya dengan
menggunakan huruf A hingga F
Konversi dari heksadesimal ke desimal
Untuk mengkonversinya ke dalam bilangan desimal, dapat menggunakan formula berikut:
Dari bilangan heksadesimal H yang merupakan untai digit hnhn − 1...h2h1h0, jika dikonversikan menjadi bilangan desimal D, maka:
Sebagai contoh, bilangan heksa 10E yang akan dikonversi ke dalam bilangan desimal:
- Digit-digit 10E dapat dipisahkan dan mengganti bilangan A sampai F (jika terdapat) menjadi bilangan desimal padanannya. Pada contoh ini, 10E diubah menjadi barisan: 1,0,14 (E = 14 dalam basis 10)
- Mengalikan dari tiap digit terhadap nilai tempatnya.
= 256 + 0 + 14
= 270
Dengan demikian, bilangan 10E heksadesimal sama dengan bilangan desimal 270



Tidak ada komentar:
Posting Komentar